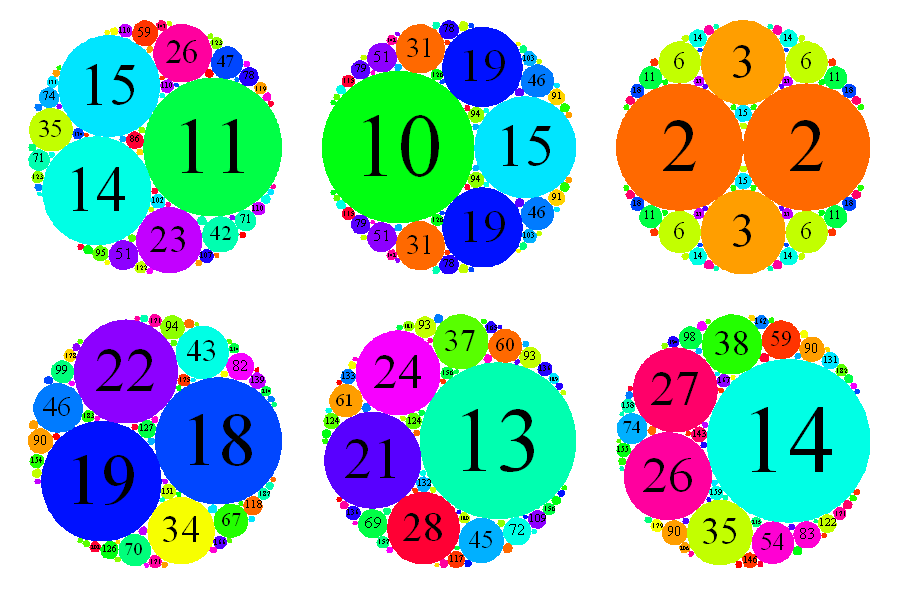
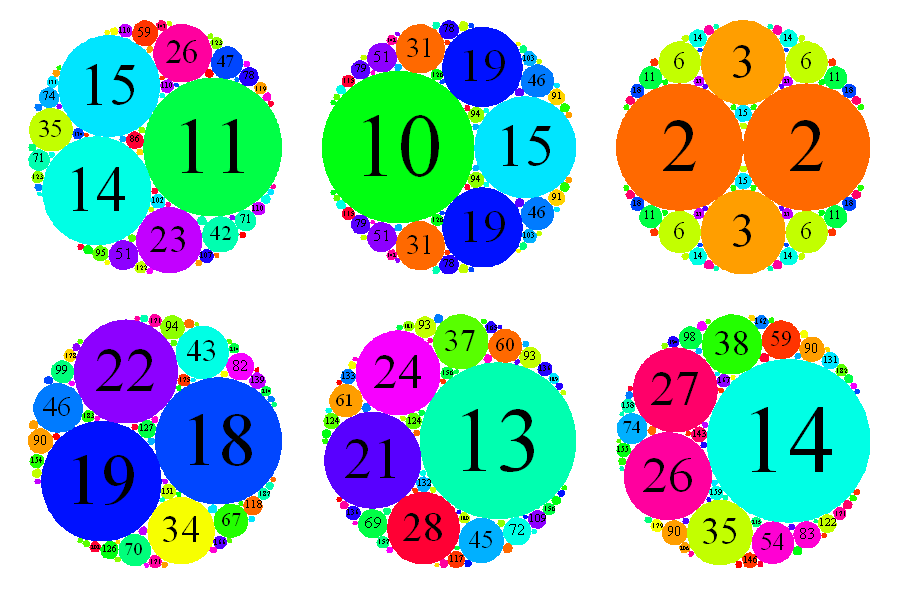
J'ai croisé plusieurs fois ces dessins sans comprendre la signification
de ces nombres.
Ces remplissages de disques à base de disques tangents ne sont pas
seulement esthétiques :
ils n'utilisent que des disques de courbures entières (inverses des rayons),
c'est elles qui sont indiquées !
Ce phénomène n'est qu'une propriété parmi tant d'autres que possèdent ces surprenantes configurations qui constituent
(avec leurs variantes spatiales) le divertissement mathématique qui m'aura le plus fasciné et passionné.
Fascination qui peut virer à une forme d'obsession maladive, prenez garde! J'ai personnellement été "contaminé" par un
mail de mon ami Maurice
Starck contenant différents liens d'apparence inoffensive :
http://mathworld.wolfram.com/SoddyCircles.html
http://mathworld.wolfram.com/ApollonianGasket.html
http://www.math.ucsd.edu/~fan/ron/papers/03_02_appolonian.pdf
https://fr.wikipedia.org/wiki/Théorème_de_Descartes
http://www.ics.uci.edu/%7Eeppstein/junkyard/tangencies/apollonian.html


Le pouvoir fascinant de ces configurations géométriques explique peut-être l'intrusion d'un prix Nobel de Chimie dans ce domaine pourtant très mathématique. Redécouvrant le théorème de Descartes sur 4 cercles 2 à 2 tangents, il en fera une poésie (!!) The Kiss precise, et étendra le résultat aux sphères. C'est en hommage à Frederick Soddy que nous nommerons Kiss un quadruplet de disques 2 à 2 tangents.
The Kiss Precise by Frederick Soddy
|
For pairs of lips to kiss maybe
Involves no trigonometry. This not so when four circles kiss Each one the other three. To bring this off the four must be As three in one or one in three. If one in three, beyond a doubt Each gets three kisses from without. If three in one, then is that one Thrice kissed internally. Four circles to the kissing come. The smaller are the benter. The bend is just the inverse of The distance form the center. Though their intrigue left Euclid dumb There's now no need for rule of thumb. Since zero bend's a dead straight line And concave bends have minus sign, The sum of the squares of all four bends Is half the square of their sum. |
To spy out spherical affairs An oscular surveyor Might find the task laborious, The sphere is much the gayer, And now besides the pair of pairs A fifth sphere in the kissing shares. Yet, signs and zero as before, For each to kiss the other four The square of the sum of all five bends Is thrice the sum of their squares. in Nature, June 20, 1936 |
Strophe ajoutée par Thorold Gosset pour décrire en dimension N le cas de N+2 hyperspheres.
The Kiss Precise (generalized) by Thorold Gosset And let us not confine our cares To simple circles, planes and spheres, But rise to hyper flats and bends Where kissing multiple appears, In n-ic space the kissing pairs Are hyperspheres, and Truth declares, As n + 2 such osculate Each with an n + 1 fold mate The square of the sum of all the bends Is n times the sum of their squares. in Nature, January 9, 1937. |
On appelle Disk de centre M et de courbure c :
À ces 2 types de régions planes ajoutons les demi-plans qui eux aussi seront appelés Disks, leur courbure étant nulle.
La Tangence dont il est question désormais est une tangence extérieure, c'est à dire que 2 Disks seront considérés comme Tangents ssi leurs frontières sont tangentes et les intérieurs des 2 Disks sont disjoints.
On appelle Kiss un quadruplet de 4 disques 2 à 2 Tangents.
Moyennant ces précisions le théorème de Soddy-Descartes sur 4 Disks 2 à 2 Tangents affirme que leurs courbures vérifient:
Le carré de la somme des 4 courbures vaut le double de la somme des carrés de ces courbures, autrement dit:
Dans un kiss, chacun des 4 Disks peut céder sa place à un unique remplaçant pour former un nouveau Kiss composée à 75% de Disks déjà en place et du remplaçant.
Mieux: la courbure du remplaçant est très simple à déterminer, si C désigne la courbure du Disk qui va être remplacé et S la somme des courbures des Disks qui restent en place alors la courbure du remplaçant est 2S-C.
C'est ce principe simple qui est à l'origine de la conservation des courbures entières.
Mieux encore : le produit de la courbure et des coordonnées des centres des Disks (quand ce ne sont pas des demi-plans) obéissent à la même règle simple de remplacement [..]
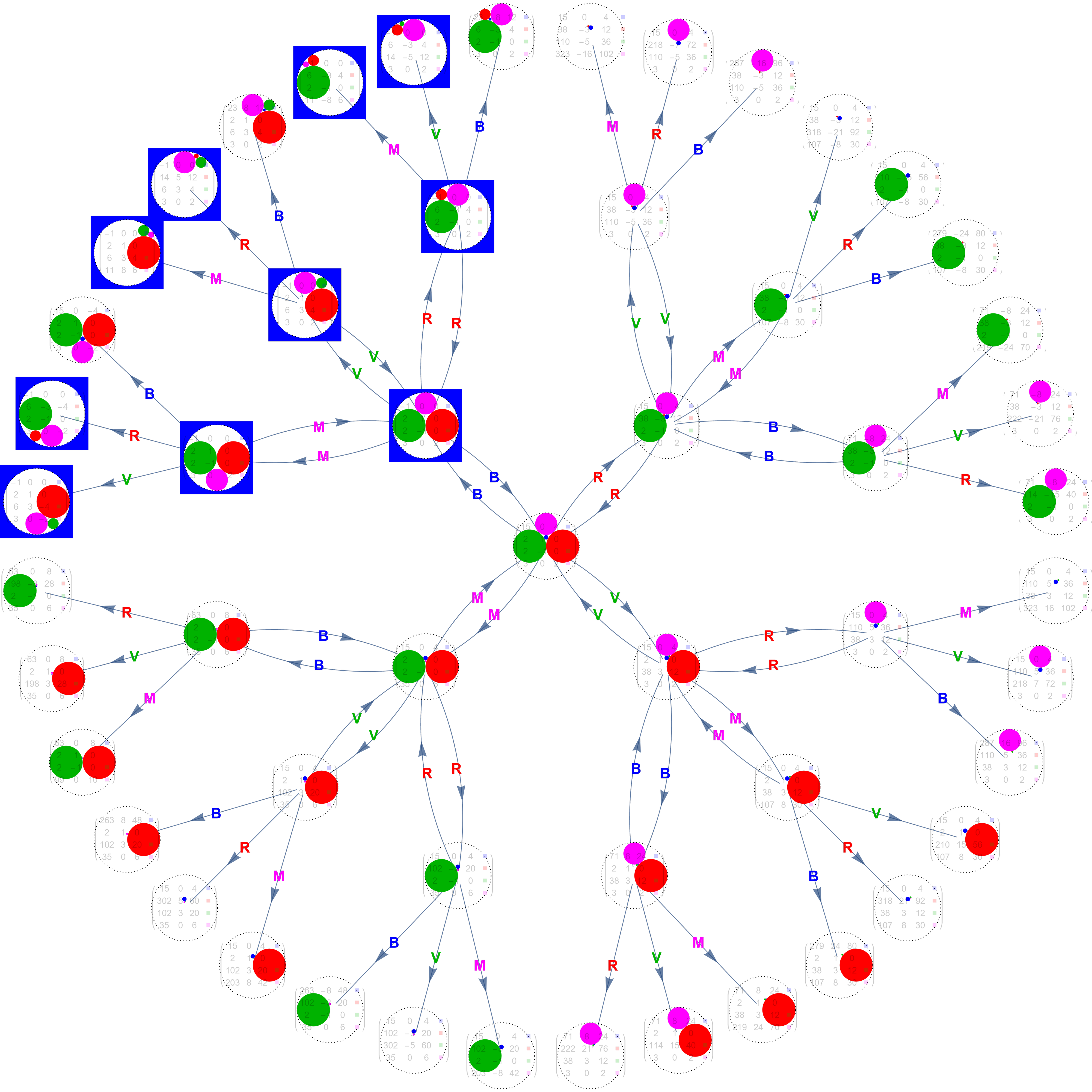
Ci-dessous un kiss initial est formé de 4 Disks Bleu, Rouge, Vert, Magenta, leur courbure est indiquée en colonne 2 du tableau.
En cliquant sur le bouton 1 ou directement sur le disque Bleu, ce dernier disparaît au profit de son remplaçant.
Cette transformation (à tester) sera appelée mutation Bleue.
Elle permet de découvrir un kiss avec un Disk de courbure négative.
En cliquant à nouveau dans la région bleue on retrouve le kiss d'origine. La mutation Bleue est donc involutive.
De même il y a 3 autres mutations possibles : Rouge, Verte et Magenta.
Une succession de mutations permet de changer considérablement le kiss initial.
L'historique des mutations est résumé par la juxtaposition des initiales des mutations au-dessus du graphique.
La chronologie des mutations se lit de droite à gauche dans ce mot écrit avec les 4 lettres B,R,V,M
Tous les disques apparaissant au fil de toutes les mutations possibles de notre kiss initial remplissent le coeur du seul disque de courbure négative.
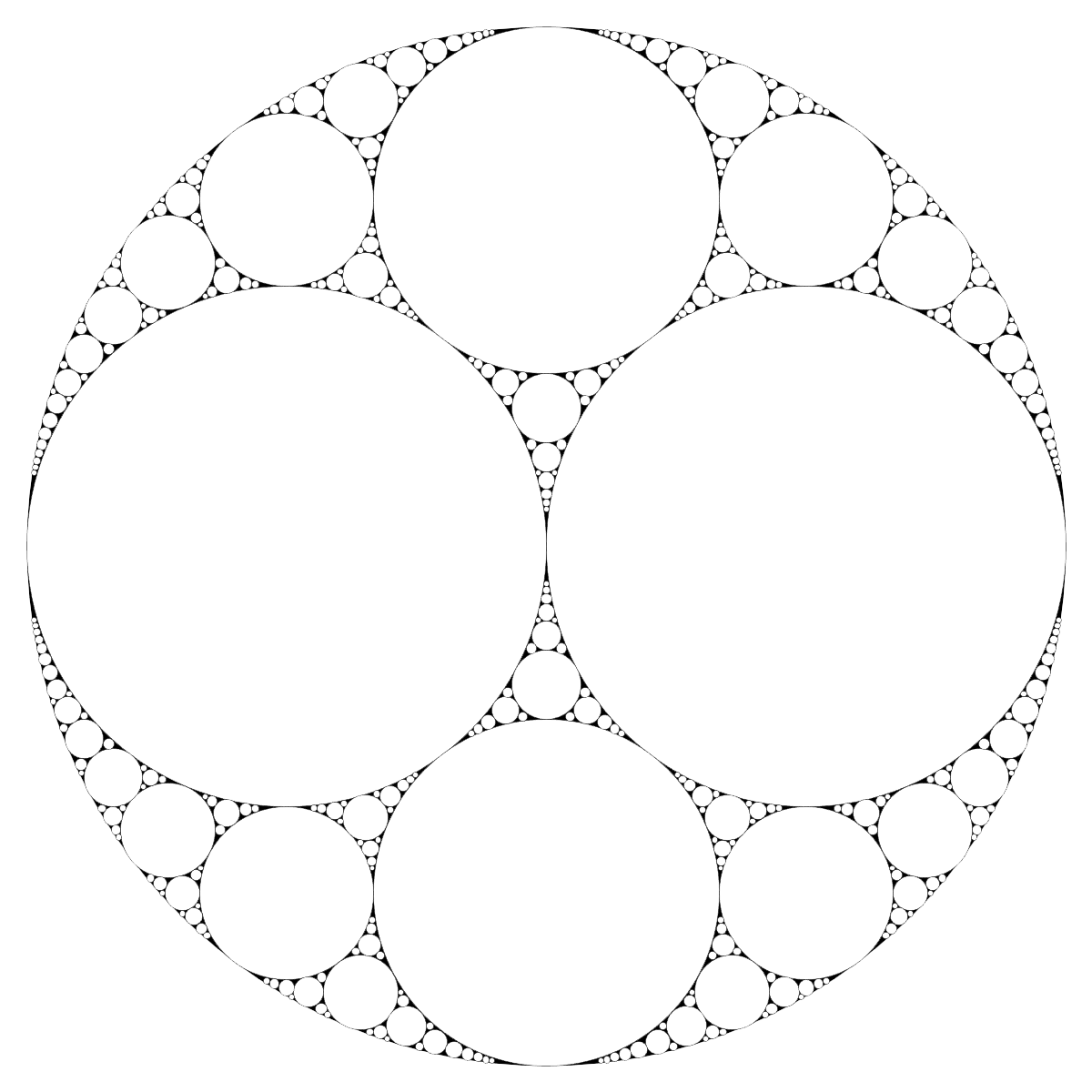
Cette structure géométrique est appelée baderne d'Appolonius, Appolonian gasket, Appolonian circle packing.
Historique des mutations : ![]()
Vous l'aurez surement deviné, le groupe G de présentation 〈 B,R,V,M | B²,R²,V²,M² 〉 agit à gauche sur l'ensemble des Kisses.
C'est ce qui est illustré ci-dessous
En filigrane, les coulisses des calculs, chaque Kiss est mémorisé sous la forme d'une matrice 4×3 au format
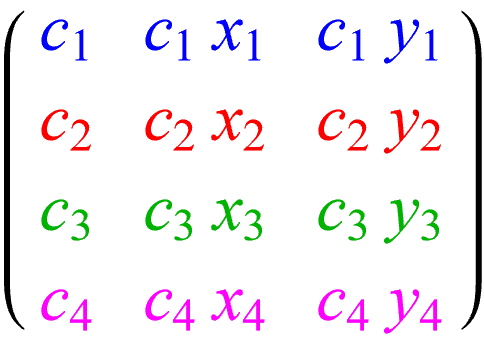
Il suffit de multiplier la matrice d'un Kiss ainsi constituée par une des 4 matrices suivantes pour obtenir les 4 mutations de ce Kiss:

En partant d'un Kiss initial dont la matrice est à coefficients entiers (comme ici), tous les calculs se font linéairement avec des entiers.
Le graphe est un arbre (ce n'est malheureusement pas le cas avec le sphere packing ce qui complique tout).
Un disque bleu mute en un disque bleu, on retrouve toujours ses coordonnées en ligne 1 dans la matrice du Kiss, de même en ligne 2,3,4 pour les disques rouges, verts magenta. Ainsi coloriés, jamais 2 disques de même couleur ne se touchent dans le packing final.[...]
Si on a bonne vue, on peut constater qu'après une chaîne de mutation, le dernier disque qui vient de muter est nouveau [...].
Si vous suivez par exemple la mutation BRB du Kiss initial, vous trouverez en périphérie du graphique un petit disque bleu qui apparaît pour la première fois.
Ce point est très important, il permet d'associer à chaque mot le nouveau disque créé à l'issue de la chaîne de mutation et ainsi mettre en bijection l'ensemble des mots (sauf le mot vide) et le packing sauf ses 4 disques initiaux.
Ceci permet d'établir un décompte du nombre de Disks créés après au plus n mutations :
L'algorithme fonctionne avec les courbures seules, c'est à dire avec la première colonne des matrices de chaque Kiss, cela ne permet pas de faire ces jolis dessins mais cela permet compter plus efficacement combien de Disks ont une courbure inférieure à un réel donné.
La suite apporte une amélioration substantielle à notre méthode pour l'optimiser et tenter un calcul approché de la dimension fractale du complémentaire de notre packing.
L'idée première est d'éviter les retours en arrière dans l'arbre des mutations (exemple ne pas faire subir une mutation bleue à un Kiss qui vient d'en subir une).
Pour cela chaque Kiss obtenu par mutation (donc tous sauf le Kiss initial) est stoké comme précédemment sous forme de matrice mais avec toujours les coordonnées du Disk qui vient de muter en dernière ligne.
Ce Kiss mutant ne devra subir que 3 mutations : celles des disques présents en ligne1, en ligne2 et en ligne3 (appelées mutations 1,2,3)
En multipliant la matrice d'un Kiss ainsi formatée, sur sa gauche par M1, M2 ou M3 (ci-dessous) on obtient ces 3 mutations.
M4 permet d'obtenir la mutation du Disk qui est en dernière ligne, elle est utile une seule fois au tout début (puisque exceptionnellement le Disk qui est stoké en dernière ligne dans la matrice du Kiss initial doit lui aussi muter).
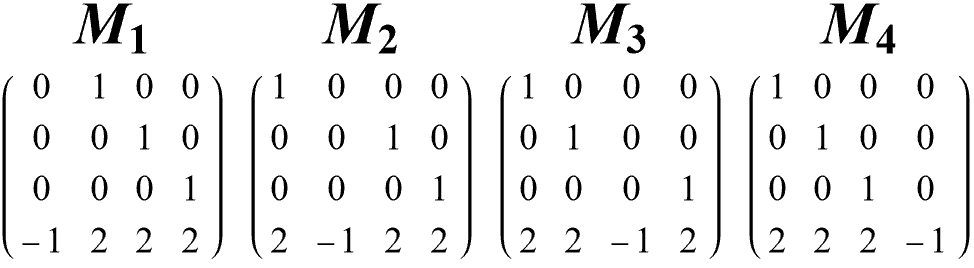
C'est extrêmement pratique car pour récolter les nouveaux disques qui apparaissent à chaque nouvelle génération, il suffit d'extraire la dernière ligne des matrices de cette nouvelle génération.
Illustration de ce nouveau principe, sur le même packing, avec cependant un Kiss initial qui a changé, nous partons désormais de Disks de courbures minimales: (-1,2,2,3)
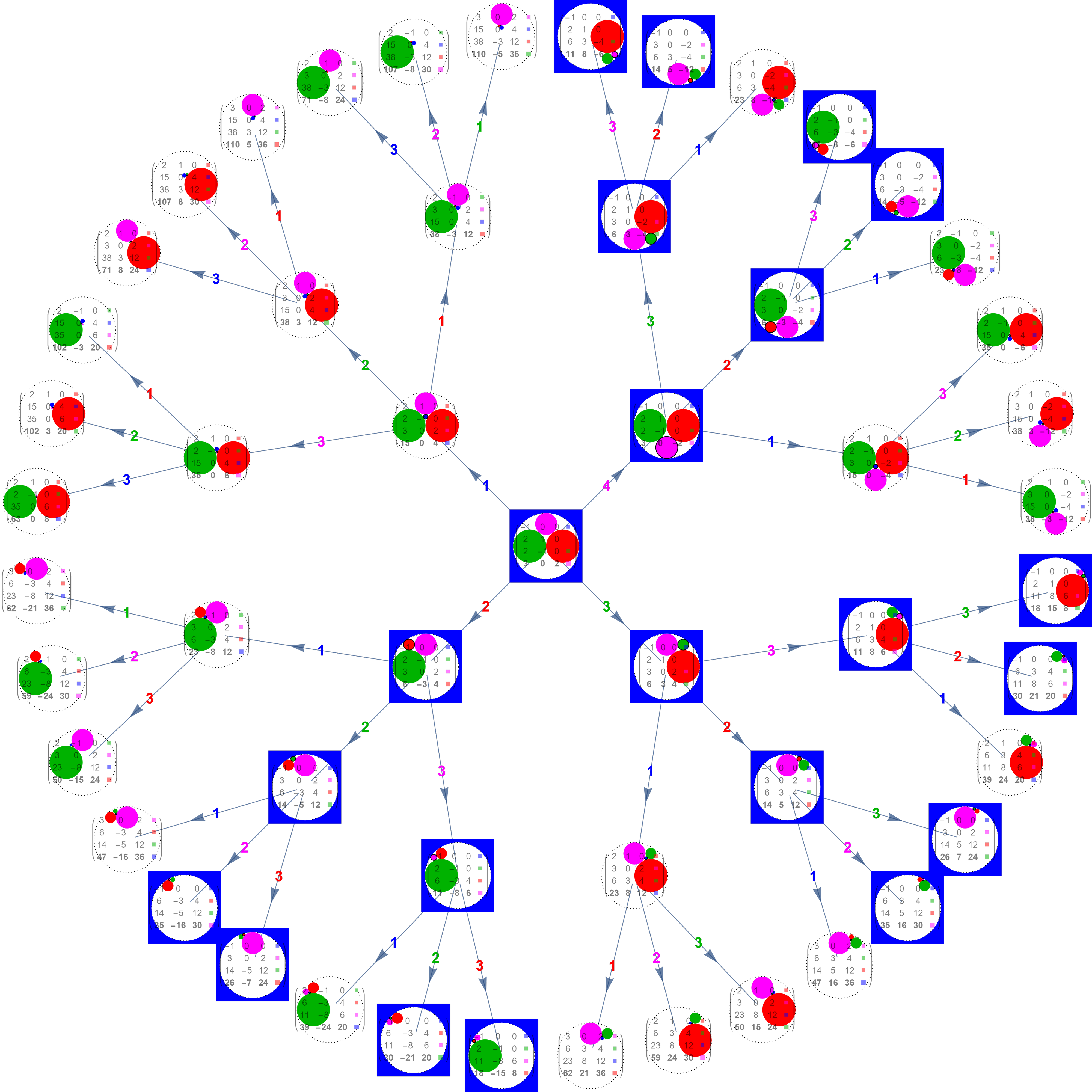
L'objectif maintenant est de dénombrer tous les disques de courbures inférieures à un entier donné N.
Commençons par remarquer que notre algorithme à base de produit matriciel fonctionne sur les colonnes de coubures seules (comme le précédent).
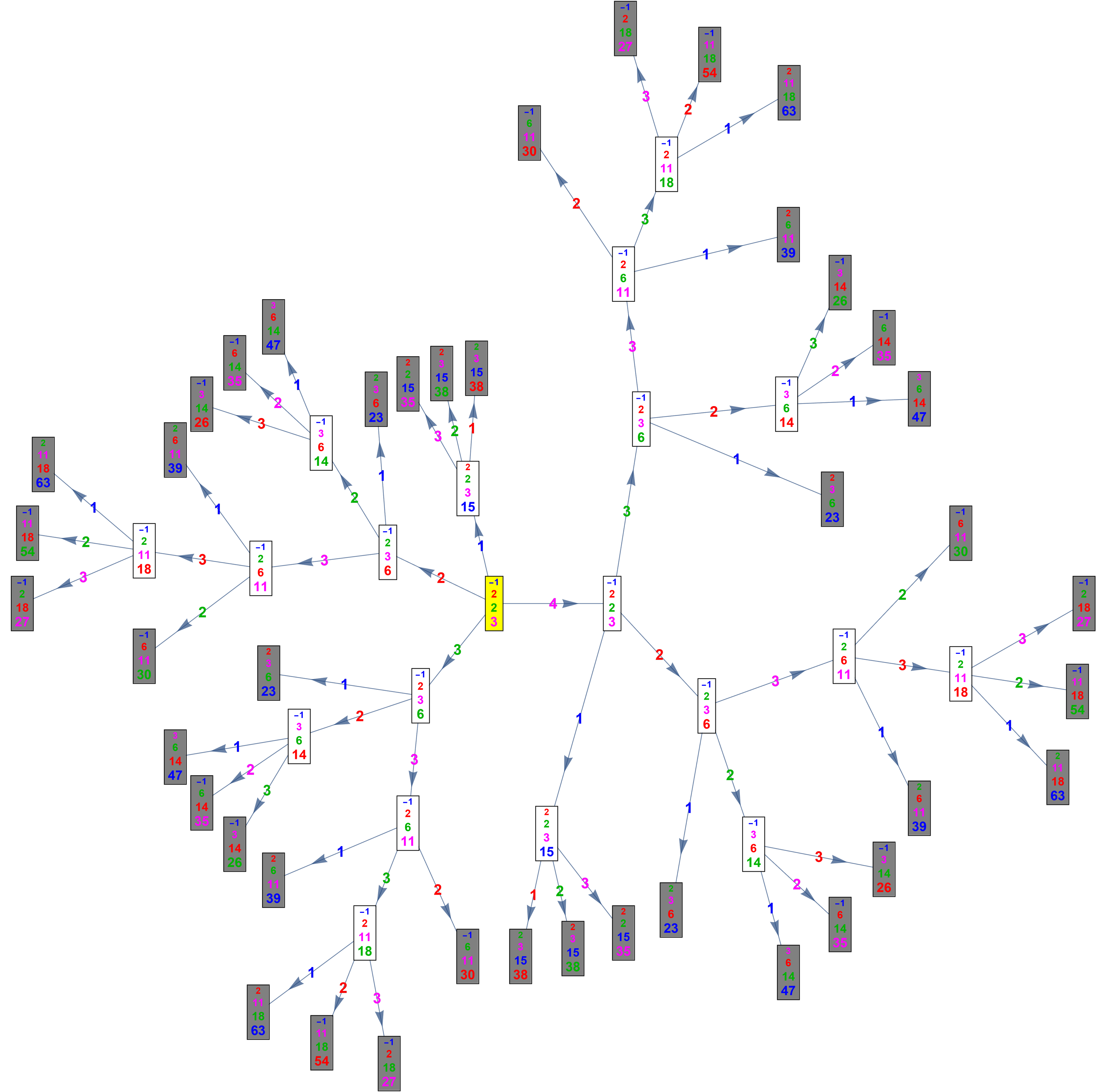
L'ensemble des quadruplets (c1,c2,c3,c4) tels que c1≤c2≤c3<c4 est stable par mutation 1,2,3 [...]
Ainsi dès lors que les 4 mutations du Kiss initial respectent cette condition (comme ci-dessus) toute leur descendance (qui s'obtient par mutations 1,2,3) aura aussi cette qualité.
Cela s'observe ci-dessus (rappelons que les courbures sont en première colonne).
La courbure qui apparaît tout en bas après une mutation 1,2,3 est strictement inférieure aux 4 courbures du Kiss qui vient de muter[...] C'est faux avec la mutation 4!
Ainsi, s'il apparaît une courbure >N, toute sa descendance ne créera que des Disks de courbures > N, on peut couper la branche.
Voici cet algorithme illustré pour trouver toutes les courbures > 20, en périphérie se trouve les nouvelles courbures qui sont ≤20, donc à ne pas comptabiliser et qui permette de couper la branche.
Nous allons utiliser l'algorithme précédent pour calculer la dimension fractale de l'ensemble ℛ des points du plan qui ne sont à l'intérieur d'aucun de nos Disks (rappelons que le Disk de courbure négative a son intérieur périphérique et il est non borné).
Voici les points qui ne sont dans aucun Disk de courbure <200, il y en a encore beaucoup à enlever, il restera toujours au moins les cercles frontières, mais parait-il qu'il y a un peu plus que ça dans ℛ [...].
ℛ est un ensemble fractal de mesure nulle.
Notons α la dimension fractale de ℛ, elle n'est pour l'heure connue qu'en valeur approchée.
Grâce à l'algorithme précédent, pour différentes valeurs de cmax on dénombre les Disks dont la courbure est <cmax.
On s'appuie sur les résultats :
limcmax→∞ ln(card(c<cmax))/ln(cmax)=α (David William Boyd 1982)
et plus récemment card(c<cmax) ~ K cmaxα où K est une constante propre à l'Appolonian-Disk-Packing (borné) considéré (Kontorovich Alex et Oh Hee 2012).
On réalise une régression affine entre ln(card(c<cmax)) et ln(cmax), α apparaît comme coefficient directeur !
